영향력 범위 분석과 최근접 분석은 모두 보로노이 하나로!

대용량 필지들에 각각 가장 가까운 역이 어디인지 매칭시켜야 하는 작업을 하던 중 더 빠르게 분석할 수 있는 방법들을 찾다가 알게 된 보로노이 다이어그램을 이용한 분석법을 공유하려합니다.

 

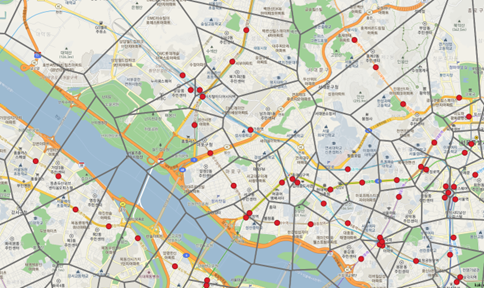
철도역 포인트를 기준으로 보로노이 분석

1. 보로노이라는 이름은 보로노이 다이어그램을 고안한 20세기 러시아 태생의 우크라이나 수학자 게오르기 페오도시예비치 보로노이의 이름에서 따왔습니다. (고안은 보로노이가 했지만 그보다 훨씬 전에 유명한 수학자이자 철학자인 데카르트에 의해 발견되었다고 추정된다고 합니다)

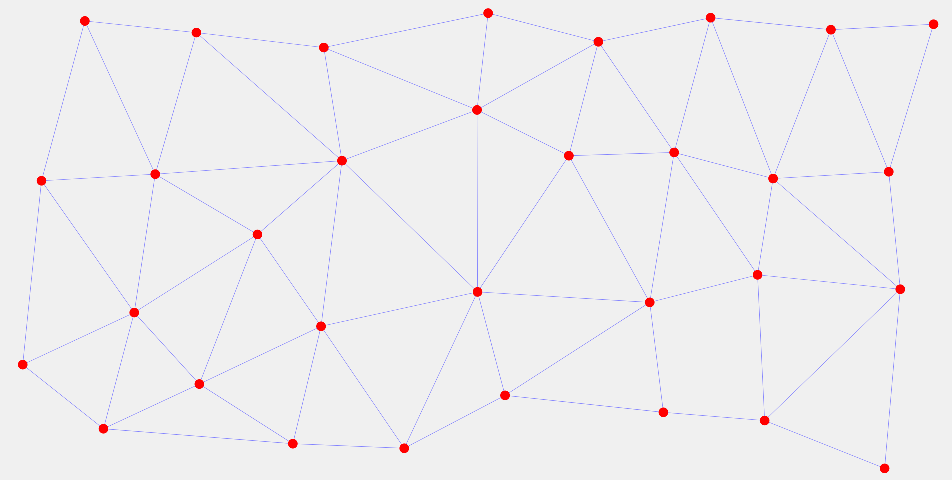
1) 종이위에 점N개를 무작위로 찍으시고 원하는 한 개의 점 (A점) 을 둘러싸고 있는 점들과 수직이등분선을 그리세요.
2) 그 수직이등분선끼리 교차되는 지점들이 A점이 만들어내는 보로노이의 꼭지점이 되며, 그 다각형이 A점을 기준으로 그려진 보로노이 다이어그램입니다.

원하는 곳에 모점을 배치 후 실행 (이미지 클릭시 링크로 이동)

학창시절 학교에서 선생님이 ‘자 주변에 쓰레기 주워라~’라고하면 내 담당 범위는 자연스럽게 나와 내 주변에 있는 애들 그 중간정도를 그린 영역을 서로 암묵적으로 생각해서 줍게 되죠. 간단히 얘기하면 이 범위가 보로노이 다이어그램입니다. 내 영향력이 가장 크게 작용하는 범위인 것이죠.

보로노이의 영향력 분석은 역학의 토대이기도 합니다. 보로노이 역학추적으로 많은 사람들을 살린 유명한 사례로 1854년 런던에 창궐했던 콜레라의 원인을 추적한 일이 있습니다. 당시 의사였던 존 스노우가 런던의 감염지도를 만들고 콜레라 발생을 관찰하며 패턴을 분석한 결과, 콜레라 희생자 다수가 브로드 거리의 특정 식수 펌프 근처에 밀집 되어있는 것을 명확히 확인할 수 있었습니다.

 

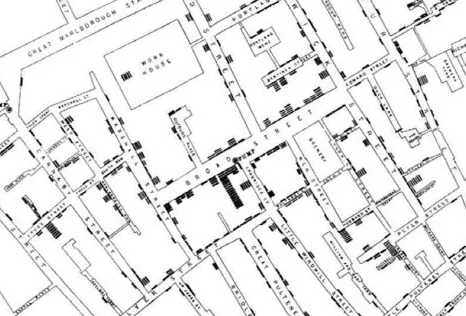
존 스노우의 콜레라 역학지도(1854)

또 영향력 분석을 통해 관할구역을 편성할 수도 있습니다. 빠른 현장 출동이 중요한 경찰서나 소방서의 위치 선정에도 보로노이 분석이 도움이 됩니다. 다만 도로의 배치나 소방인원 등의 요소 등 영향력에 포함해서 생각해야할 부분도 많겠죠. 그러한 가중치들을 포함해서 분석하는 방법도 있습니다.

모점이 가중치가 다를 때 그 가중치를 포함해서 보정된 보로노이 분할하는 것도 가능합니다. 예를 들어 학군을 검토하는 경우라면, 학교의 수용가능 인원수나 학교 주변의 아동수 등 다양한 조건을 조합해 가중치를 설정한 다음, 가중치가 있는 보로노이 분할을 하면 기본적인 보로노이 보다 이상적인 결과에 접근할 수 있습니다. 다만 작성방법이 까다롭고 원하는 요소가 다양하기 때문에 가중치를 포함한 보로노이 분할은 심화된 지식과 전문지식을 필요로 합니다.

보로노이 분할이나 보로노이 다이어그램은 가까운 역이나 최단 루트를 찾을 때도 사용됩니다. 앞서 말했듯이 각 토지에서 제일 가까운 역이 어딘지 입력할 때 해당 기능을 이용했습니다. 역 포인트를 기준으로 보로노이 폴리곤을 작성한 후 작성된 폴리곤과 같은 좌표에 있는 토지들을 결합시켜 역정보를 입력해주었습니다.

또 서로 맞대고 있는 보로노이 폴리곤끼리 따라가다보면 최단 루트도 찾을 수도 있습니다. 물론 이 경우도 도로의 배치 등이 같이 고려되어야겠지만요.

GIS SW의 보로노이 분할 기능을 사용하면 모점군에서 자동으로 보로노이 다이어그램을 작성해주므로 분석 시에 편리합니다.
기능의 위치는 [QGIS] – [공간 처리 툴박스] – [백터 도형] – [보로노이 폴리곤] 이며

 

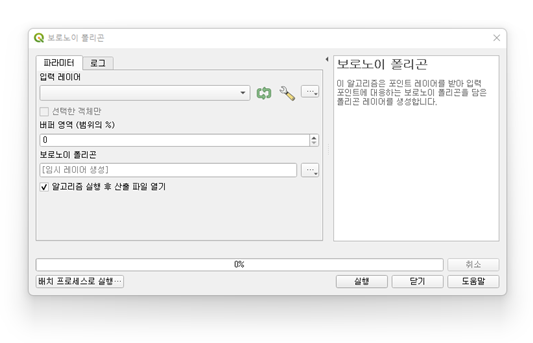
위의 그림에서 입력레이어에 분석하고자 하는 포인트 레이어를 넣고 실행하면 대응되는 보로노이 폴리곤이 자동으로 생성됩니다.

제가 소개해드릴 내용은 여기까지입니다. 이름도 그리는 방법도 어려워보이지만 사실 예술,건축 뿐만이 아니라 잠자리 날개에도 기린의 무늬에도 나타나 있듯 자연스러운 도형이면서 실생활에 밀접하게 연관되어 있습니다. 이 칼럼을 계기로 여러분도 이 방법을 공간 분석하는데 잘 활용해주시면 뿌듯할 것 같습니다. 다음에도 간단하지만 쓸모있는 분석방법이 있다면 모두와 공유하러 돌아오겠습니다.